买卖股票的最佳时机
买卖股票的最佳时机
给定一个数组,它的第 i 个元素是一支给定股票第 $i$ 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
没什么好说的,brute-force 的方法也没见的坏到哪里去。巧妙一点的方法可以用两个数组 min 和 max 缓存从 $[0,i]$ 的最小值和 $[i,N-1]$ 的最大值。
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.empty()) return 0;
int N = (int)prices.size();
vector<int> min_vec(N, prices[0]);
vector<int> max_vec(N, prices[N-1]);
for (int i = 1; i < N; ++i) {
min_vec[i] = min(min_vec[i-1], prices[i]);
max_vec[N-i-1] = max(max_vec[N-i], prices[N-i-1]);
}
int res = 0;
for (int i = 0; i < N; ++i)
res = max(res, max_vec[i] - min_vec[i]);
return res;
}
};
买卖股票的最佳时机 II
给定一个数组,它的第 i 个元素是一支给定股票第 $i$ 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
多次交易,可以用自动机来模拟,两个状态 $A=\text{持有股票} $和 $B=\text{不持有股票}$,状态转移为 ${A \overset{\text{sell}}{\longrightarrow} B, A \longrightarrow A, B \overset{\text{buy}}{\longrightarrow} A, B \longrightarrow B }$. $A$ 和 $B$ 都存储到目前为止是这个状态的时候能获得的最大利润,显然这个过程是马尔可夫的,只取决于前一个状态的值,所以可以用类似DP的方式解决
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.empty()) return 0;
int has = -prices[0], empty = 0;
for (size_t i = 1; i < prices.size(); ++i) {
has = max(has, empty - prices[i]);
empty = max(empty, has + prices[i]);
}
return max(0, max(has, empty));
}
};
买卖股票的最佳时机 III
给定一个数组,它的第 $i$ 个元素是一支给定的股票在第 $i$ 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这个情况下, 没有交易完成, 所以最大利润为 0。
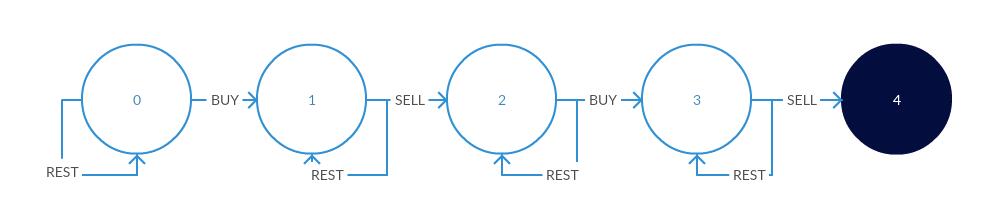
依然是自动机,定义略有不同
| State | Definition |
|---|---|
| 0 | 初始状态 |
| 1 | 第一次买入股票 |
| 2 | 第一次卖出股票 |
| 3 | 第二次买入股票 |
| 4 | 第二次卖出股票 |
0状态对应的值始终是0,不需要变量存储,注意状态 $s$ 只有在 $i\geq s$ 的时候的更新才是 valid 的,所以注意这里的初始值和之前不同
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.empty()) return 0;
int N = (int)prices.size();
int e1 = -prices[0], e2 = INT_MIN, e3 = INT_MIN, e4 = INT_MIN;
for (int i = 1; i < N; ++i) {
e1 = max(e1, -prices[i]);
e2 = max(e2, e1 + prices[i]);
e3 = max(e3, e2 - prices[i]);
e4 = max(e4, e3 + prices[i]);
}
return max(0, e4);
}
};
买卖股票的最佳时机 IV
给定一个数组,它的第 $i$ 个元素是一支给定的股票在第 $i$ 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 $k$ 笔交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
就是上面那种情况的推广,注意做了一个优化,当 $2k > len(pricse)$ 的时候可以直接按照贪心来做了(每回合都可以进行交易),因为测试用例会有 $2k \gg len(prices)$ 的情况,这个时候会OOM.
class Solution {
private:
int getWeight(int i) {
return (i % 2) * 2 - 1;
}
public:
int maxProfit(int k, vector<int>& prices) {
if (prices.empty() || k == 0) return 0;
if (2 * k > (int)prices.size()) {
int res = 0;
for (size_t i = 0; i < prices.size()-1; ++i) {
if (prices[i] < prices[i+1])
res += prices[i+1] - prices[i];
}
return res;
}
vector<int> buff(2 * k, INT_MIN);
buff[0] = -prices[0];
for (size_t i = 1; i < prices.size(); ++i) {
buff[0] = max(buff[0], -prices[i]);
for (size_t j = 1; j < buff.size(); ++j)
buff[j] = max(buff[j], buff[j-1] + getWeight(j) * prices[i]);
}
return max(0, buff.back());
}
};
最佳买卖股票时机含冷冻期
给定一个整数数组,其中第 $i$ 个元素代表了第 $i$ 天的股票价格
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:
输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
就是多了一种状态而已
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.empty()) return 0;
vector<int> has(prices.size(), 0);
vector<int> empty(prices.size(), 0);
vector<int> cold(prices.size(), 0);
has[0] = -prices[0];
for (size_t i = 1; i < prices.size(); ++i) {
has[i] = max(has[i-1], empty[i-1] - prices[i]);
cold[i] = has[i-1] + prices[i];
empty[i] = max(empty[i-1], cold[i-1]);
}
int result = max(has.back(), cold.back());
return max(result, empty.back());
}
};
买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中第 $i$ 个元素代表了第 $i$ 天的股票价格 ;非负整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每次交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
示例 1:
输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
注意:
- 0 < prices.length <= 50000.
- 0 < prices[i] < 50000.
- 0 <= fee < 50000.
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
if (prices.empty()) return 0;
int empty = 0, has = -prices[0];
for (size_t i = 0; i < prices.size(); ++i) {
has = max(has, empty - prices[i]);
empty = max(empty, has + prices[i] - fee);
}
return max(empty, 0);
}
};