泛函

设 $\mathbb{C}$ 是一个由函数组成的集合，$\mathbb{B}$ 为数集，称 $F: \mathbb{C} \rightarrow \mathbb{B}$ 为泛函 (functional), 记作 $F = F[y(x)]$.

一般情况下泛函式常用积分形式表示:

$$F[y(x)] = \int_{x_0}^{x_1}G(y,y',x)dx,$$

其中被积函数 $G$ 称为核

例1 两点之间最短路径

从点 $(x_1, y_1)$ 到 $(x_2, y_2)$ 的一条曲线为 $y = y(x)$. 找出长度最短的一条曲线.

在曲线上取微元有: $ds^2 = dx^2 + dy^2 \Rightarrow ds = \sqrt{1 + (\dfrac{dy}{dx})^2}dx$

曲线的总长: $s = \int_{x_1}^{x_2}\sqrt{1 + y’^2}dx$

问题变为: $y^{*}(x) = \underset{y}{\arg\min}\ s[y]$.

例2 最速降线

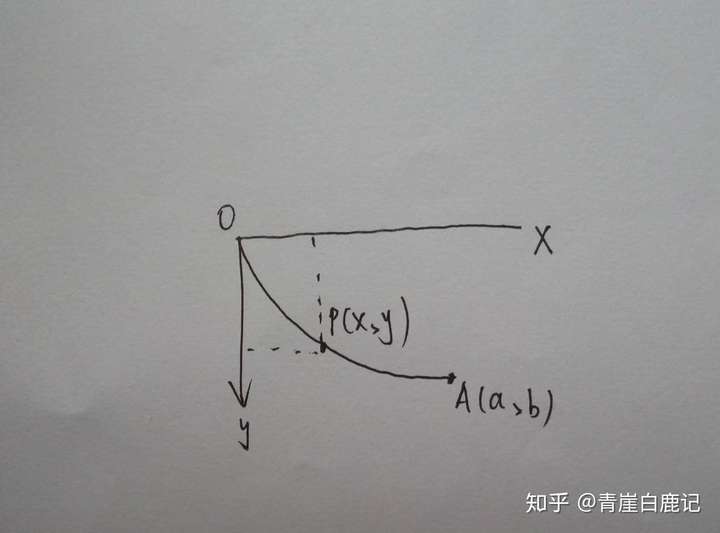
物体运动到y时，失去的势能是 $mgy$, 得到的总动能为 $mv^2/2$. 根据能量守恒有: $v = \sqrt{2gy}$.

在曲线点 $(x,y)$ 处，运动速度定义为 $v = \dfrac{ds}{dt} = \dfrac{\sqrt{1 + y’^2}dx}{dt}$.

从而有关系 $dt = \dfrac{\sqrt{1 + y’^2}dx}{v} = \sqrt{\dfrac{1 + y’^2}{2gy}}dx$.

得到

$$t = \int_0^{a}\sqrt{\dfrac{1 + y'^2}{2gy}}dx$$

从而 $y^* = \underset{y}{\arg\min}\ t[y]$

基本概念

类函数：具有某种共同性质的函数集合，记作 $\mathbb{F}$。例如在最速降线的例子中所有曲线都通过 $O, A$

如果一个类函数中的某个函数能够使某个泛函取得极值或可能取得极值，则该类函数称为变分问题的可取类函数。可取类函数中的函数有无穷多个，其中任何一个都称为可取函数。类函数中能使泛函取得极值或可能取得极值的函数或曲线称为极值函数，也称为变分问题的解。变分法的核心问题就是求解泛函的极值函数和极值函数对应的泛函极值。如果可取曲线类的曲线端点预先给出且为定值，则所求泛函极值的问题称为固定端点变分问题。

引理

Lemma-1

如果函数 $f(x)$ 在 $[a,b]$ 内连续，$\eta(x)$ 是满足 $\eta(a) = \eta(b) = 0$ 的任意函数，若

$$\int_a^b f(x)\eta(x)dx = 0,$$

总是成立，则 $f(x)$ 在 $[a,b]$ 上满足 $f(x) = 0$.

Proof. 设 $f(x)$ 在 $[a,b]$ 上不恒为0，取 $\eta(x) = -f(x)(x-a)(x-b)$, 有

$$\int_a^b f(x)\eta(x)dx = \int_a^b f^2(x)(x-a)(b-x) > 0$$

Lemma-2

若 $f(x), g(x)$ 在 $[a,b]$ 内连续，$\eta(x), \xi(x)$ 是满足 $\eta(a) = \eta(b) = \xi(a) = \xi(b) = 0$ 的任意函数，若

$$\int_a^b\left[ f(x)\eta(x) + g(x)xi(x) \right]dx = 0$$

则有 $f(x) = g(x) = 0,\ \forall x\in [a,b]$. 证明方法同上

函数的变分

对于任意 $x\in[x_0, x_1]$ ，可取函数 $y(x)$ 与另一个可取函数 $y_0(x)$ 的差称为函数 $y$ 在 $y_0$ 处的变分，或者叫函数的变分，记作 $\delta y$, 其中 $\delta$ 为变分算子，有：

$$\delta y = y(x) - y_0(x) = \epsilon \eta(x).$$

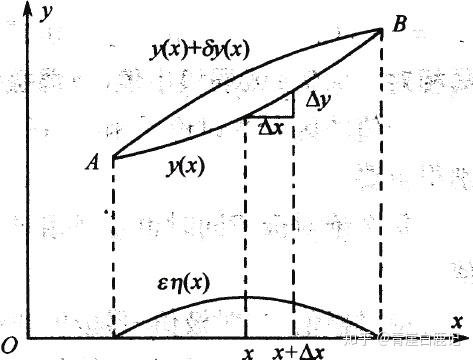
这里注意一下函数的变分 $\delta y$ 与函数的增量 $\Delta y$ 之间的区别，如图所示：

• 函数的变分 $\delta y$ 是两个不同的函数在自变量x固定时的差，函数发生了改变。
• 函数的增量 $\Delta y$ 是自变量 $x$ 的增量使得函数 $y(x)$ 产生的增量，函数依然是原来的函数。

最简泛函的变分

设 $G(y,y’,x)$ 是三个独立变量 $y(x), y’(x), x$ 在区间 $[x_0, x_1]$ 上的已知函数，且二阶可微，其中 $y, y’$ 是 $x$ 的未知函数，则泛函

$$F[y] = \int_{x_0}^{x_1} G(y,y',x)dx$$

称为最简泛函，$G$ 为最简泛函的核

令 $y_1 = y + \epsilon \eta(x)$, $y’_1 = y’ + \epsilon \eta’(x)$, 有（下面为简洁起见，略去积分边界 $[x_0, x_1]$ ）

$$F[y_1] = \int G(y_1, y'_1, x)dx = \int G_1dx = \phi(\epsilon)$$

在 $\epsilon = 0$ 附近进行泰勒展开有

$$\phi(\epsilon) = \phi(0) + \phi'(0)\epsilon + O(\epsilon^{2})$$

而

$$\phi(0) = F[y], \phi(\epsilon) = F[y+\epsilon\eta]$$

从而

$$\Delta F = F[y + \epsilon\eta] - F[y] = \phi'(0)\epsilon + O(\epsilon^2)$$

而

$$\begin{split} \phi'(0) &= \dfrac{\partial}{\partial \epsilon}\left( \int G_1dx \right)\Bigg|_{\epsilon=0} \\ &= \int \left( \dfrac{\partial G_1}{\partial \epsilon} \right)\Bigg|_{\epsilon=0}dx \\ &= \int \left( \dfrac{\partial G_1}{\partial y_1} \dfrac{\partial y_1}{\partial \epsilon} + \dfrac{\partial G_1}{\partial y'_1} \dfrac{\partial y'_1}{\partial \epsilon} \right)\Bigg|_{\epsilon=0}dx \\ &= \int \left( \dfrac{\partial G_1}{\partial y_1} \eta + \dfrac{\partial G_1}{\partial y'_1} \eta' \right)\Bigg|_{\epsilon=0}dx \\ &= \int \left( \dfrac{\partial G}{\partial y} \eta + \dfrac{\partial G}{\partial y'} \eta' \right)dx \end{split}$$

将$\epsilon\phi’(0)$ 记为泛函的一阶变分，记作 $\delta F$

从而

$$\begin{split} \Delta F &= \delta F + O(\epsilon^2) \\ \delta F &= \epsilon\int \left( \dfrac{\partial G}{\partial y} \eta + \dfrac{\partial G}{\partial y'} \eta' \right)dx \end{split}$$

我们需要将泛函的“微分式” 一般微分式进行类比，在另一种定义中，我们将 $\dfrac{\delta F}{\delta y}$ 定义为泛函的一阶导数，上面的式子定义为

$$\Delta F = \epsilon\int\dfrac{\delta F}{\delta y}\eta dx + O(\epsilon^2)$$

变分和泛函导数的关系为

$$\delta F = \epsilon\int\dfrac{\delta F}{\delta y(x)}\eta(x)dx$$

而此时我们手中的式子为

$$\Delta F = \epsilon\int\left( \dfrac{\partial G}{\partial y} \eta + \dfrac{\partial G}{\partial y'} \eta' \right) dx + O(\epsilon^2)$$

我们需要将上述式子中的 $\eta$ 提取出来，将上面的积分分开，对第二部分进行分部积分

$$\begin{split} \delta F &= \int \left( \dfrac{\partial G}{\partial y} \eta + \dfrac{\partial G}{\partial y'} \eta' \right)dx \\ &= \int \left( \dfrac{\partial G}{\partial y} \eta \right)dx + \int \left( \dfrac{\partial G}{\partial y'} \eta' \right)dx \\ &= \int \left( \dfrac{\partial G}{\partial y} \eta \right)dx + \dfrac{\partial G}{\partial y'}\eta\Bigg|_{x_0}^{x_1} - \int \left( \dfrac{d}{dx}\left(\dfrac{\partial G}{\partial y'}\right) \eta \right)dx \\ \end{split}$$

而已知 $\eta(x_0) = \eta(x_1) = 0$, 从而

$$\delta F = \int \left( \dfrac{\partial G}{\partial y} - \dfrac{d}{dx}\left(\dfrac{\partial G}{\partial y'}\right) \right)\eta dx$$

而使得泛函取得极值的时候应该有 $\delta F = 0$, 从而在 $[x_0, x_1]$ 上有

$$\int_{x_0}^{x_1} \left( \dfrac{\partial G}{\partial y} - \dfrac{d}{dx}\left(\dfrac{\partial G}{\partial y'}\right) \right)\eta dx = 0$$

根据Lemma-1, 有在 $[x_0, x_1]$ 上

$$\dfrac{\partial G}{\partial y} - \dfrac{d}{dx}\left(\dfrac{\partial G}{\partial y'}\right) = 0$$

上式即为 Euler-Lagrange equation.